Tulang nin Ishango
| Tulang nin Ishango | |
|---|---|
| Os d'Ishango (Pranses) | |
 An tulang nin Ishango, nakatampok sa sarong museo sa Belhika. | |
| Materyales | Tulang (pibula kan papyo), kuwarso |
| Laba | 10 sentimetro[1] |
| Panahon/Peryudo/kultura | Halangkaw na Paleolitiko (c. 18,000 BK.-20,000 BK.) |
| Nadiskubre | 1950 sa laog kan Nasyunal na Parke nin Virunga, Goma, Demokratikong Republika kan Kongo[1] 0°7′37″S 29°36′2″E / 0.12694°S 29.60056°E |
| Nadiskubre ni | Jean de Heinzelin de Braucourt |
| Kinamumugtakan sa ngunyan | l’Institut Royal Belge des Sciences Naturelles, Bruselas, Belhika.[1] |
| Tagboan | 50°51′22″N 4°25′33″E / 50.8562°N 4.4258°ETagboan: 50°51′22″N 4°25′33″E / 50.8562°N 4.4258°E |
| Astronomical and World Heritage Webportal | |
An tulang nin Ishango (Ingles: Ishango bone) sarong kagamitang gibo sa tulang na may laba na 10 sentimetro.[1] asin pigtutubudan na saro man na kagamitang matematikal. Pigtatanyang pighimo ini kadtong panahon nin Halangkaw na Paleolitiko, an tulang iyo an pibula kan sarong papyo[2] na igwang matarom na pidaso nin kuwarso sa saro sa mga puro kaini, pwede para sa pag-uukit. Pigtutubudan na piggamit ini bilang sarong pantalâ (tally stick) kan pipira, huli man ta igwang sarong serye nin mga kurit na nakalaag digdi na ipigsasaboot na mga talang panmarkang pig-ukit sa tolong raya. Dai pig-uuyunan ini kan pipira, na nagsasaboot man na pwedeng piggibo an mga kurit na ini tanganing urog na pasil na kaputan o dai baga tanganing sa iba pang mga rason na daing kinaaraman sa matematika.[3] Pigsasabi kan mga pabor sa pagiging bagay pangmatematika kaini na an mga nakalaag na marka digdi dai pig-ukit sana ning basta-basta asin pwedeng piggamit bilang pambilang asin pangkalkula kan mga simpleng operasyon nin matematika.[4][5]
Nahiling kan Belhikanong si Jean de Heinzelin de Braucourt an tulang nin Ishango kadtong 1950 mantang binabaklay an Belhikanong Kongo (sakop ngunyan kan Kongo DR).[6] Nadiskubre ini sa laog kan Nasyunal na Parke kan Virunga, harani sa Goma, Kongo DR.[1] Hali an tubig kan naturang salog sa Danaw nin Edward asin saro sa mga panginot na salog na nagsusuplay nin tubig sa Salog Nilo. Nahiling an naturang tulang sa sarong inabandonang saditon na iniirukan kan mga parasira na natalbungan kan sarong pagtuga nin bulkan.[7]
Inot na tantyang hali an tulang bandang 9,000 BK asin 6,500 BK.[8] Iyo pa man, kan tinatya utro an lugar kung sain ini nadukayan, napag-araman na maabot sa 20,000 taon na an gurang kaini (nasa tanga kan 18,000 BK sundo sa 20,000 BK).[9]
Nasa sarong permanenteng eksibisyon an tulang sa l’Institut Royal Belge des Sciences Naturelles[lower-alpha 1] sa Bruselas sa Belhika.[1]
Pagpapasabot
[baguhon | baguhon an source]
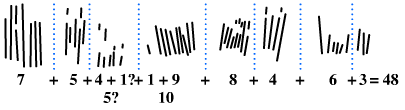


Nasa tolong hanay an mga ukit sa tulang, kung sain grinupo ini ning di-pantay, na naghatod nin "kadakol na mga hinuhang nakakapanabik" huli ta pwede an boot sabihon kaini na igwang aram na sa mga desimal o panginot na bilang an mga suanoy na tawo. Bagaman igwa nin pirang kumukwestyon sa mga ini, pigkokonsidera kan pirang siyentipiko na piggamit ini para sa mga simpleng operasyon nin matematikal o dai daw sa pagmukna nin sarong sistema nin pagbilang.[5]
Pwedeng iinterpreta an ikatolong hanay bilang sarong "talahanayan ng mga pangunahing bilang,"[7] alagad pwede nagkataon sana an pagkakagrupo kaini.[5] Ipinagpalagay kan historyador sa matematika na si Peter S. Rudman na dai pa ganap na nasasabutan an konsepto kan mga panginot na bilang sagkod sa pag-abot kan 500 BK, asin nagdedepende sa konsepto kan pagbabanga, na pigtutubudan niyang nadiskubre kang dai maamay pa sa 10000 BK.[3]
Mantang ipinagpalagay man ni Alexander Marshack na ginamit an tulang bilang sarong anom na bulan na kalendaryong lunar.[10] Nin huli digdi, nagtao nin sarong opinyon si Claudia Zaslavsky na an naggibo kan tulang pwedeng sarong babae, na pwedeng nagbase sa regla asin an kinaaraman kaini kan pagbago kan lalawgon kan bulan sa langit.[11] Pigkontra ini kan sarong pag-aadal dangan pigsabing masyadong ininterpreta ni Marshack an mga datos. Dagdag pa kaini, dai pigsusuportahan kan ebidensiya an hinuhang kalendaryong lunar.[12]
Dai pa sana nahaloy, nagtao nin sarong suhestiyon si Vladimir Pietser na baka piggamit an tulang bilang sarong kagamitan sa pagbilang na igwa nin báse na 12 asin pang-irarom na báse na 3 asin 4, kung sain pwede man na piggamit ini sa pagpapadakol. Kinumpara niya ini sa sarong primitibong slide rule.[4]
Pigsabi man ni Caleb Everett na "dai barabastang pig-ukit" an mga nakalaag sa tulang, asin pwedeng saro ining ebidensiya nin pagkakaigwa nin mga suanoy na bilang. Iminungkahi niya na an enot na hanay, pwedeng "pagkakaarog kan pagdoble" asin pwedeng piggamit ini sa pagbibilang asin pagpapadakol na iyo man na bilang sarong "giya sa pagbilang."[5]
Ikaduwang tulang
[baguhon | baguhon an source]Kadtong nagkalot man sa parehas na lugar kadtong 1959, igwa pang nahiling na sarong tulang. Urog na magian an arok o kolor kaini kaysa sa nainot, kinayod, pinapayat, asin pinakinis. Igwa man ining gatak sa sarong puro, na nagbunyag na guwang (hollow) ini. Pwedeng igwa man ining kuwarsong nakalaag arog kan nainot na tulang, o pwede man na saro ining pangkapot. Igwang 90 ukit sa anim na bahagi ang butong ito na may habang 14 na sentimetro. Kinategorya an mga ukit na nahiling sa duwa: "panginot" asin "menor," na pigbase base sa laba kan lambang ukit. Ipinagpalagay ni Jean de Heinzelin na mga yunit o dai daw mga lakdang (multiple) an mga panginot na ukit asin mga bangambilang man o sararadit na yunit an mga menor na ukit. Nagtutubod siya na sarong "paribay-ribay na panukol sa mga báse na 10 asin 12" an mga tulang.[13]
Hilingon man
[baguhon | baguhon an source]Mga toltolan
[baguhon | baguhon an source]Mga pinagkuanan
[baguhon | baguhon an source]- ↑ 1.0 1.1 1.2 1.3 1.4 1.5 "The Ishango bone, Democratic Republic of the Congo" [Ang Buto ng Ishango, Republikang Demokratiko ng Kongo]. UNESCO Astronomy and World Heritage Webportal (in English). Retrieved Disyembre 5, 2020. Unknown parameter
|url-status=ignored (help); Check date values in:|access-date=(help) - ↑ "A very brief history of pure mathematics" [An haliputon na uusipon kan purong matematika]. University of Western Australia - School of Mathematics (in English). Archived from the original on Hulyo 7, 2008. Retrieved Disyembre 2, 2020. Check date values in:
|access-date=, |archive-date=(help) - ↑ 3.0 3.1 Rudman, Peter Strom (2007). How Mathematics Happened: The First 50,000 Years [Pano nangyari an Matematika: An Enot na 50,000 Taon] (in English). Prometheus Books. p. 63. ISBN 978-1-59102-477-4.
- ↑ 4.0 4.1 Pletser, Vladimir (Abril 4, 2012). "Does the Ishango Bone Indicate Knowledge of the Base 12? An Interpretation of a Prehistoric Discovery, the First Mathematical Tool of Humankind" [Ipinapahiling daw kan Tulang nin Ishango an Kaaraman sa ika-12 Base? Sarong interpretasyon sa Suanoy na Pagdiskubre, an Enot na Kagamitan nin Matematikal kan Sangkatawuhan]. arXiv (in English). Retrieved Disyembre 5, 2020. Check date values in:
|access-date=, |date=(help) - ↑ 5.0 5.1 5.2 5.3 Everett, Caleb (2017). Numbers and the Making of Us: Counting and the Course of Human Cultures [An mga Bilang asin an Paghimo satuya: Pagbibilang asin an Sulog kan Kultura kan mga Tawo] (in English). Harvard University Press. pp. 35–36. ISBN 9780674504431.
- ↑ de Heinzelin, Jean (Hunyo 1962). "Ishango". Scientific American. Vol. 206 no. 6. p. 105-116. Check date values in:
|date=(help) - ↑ 7.0 7.1 Williams, Scott W. "Mathematicians of the African Diaspora" [Mga Matematiko kan Aprikanong Pagwarak]. State University of New York - Buffalo (in English). Retrieved Disyembre 5, 2020. Unknown parameter
|url-status=ignored (help); Check date values in:|access-date=(help) - ↑ Gerdes, Paulus (1991). "On The History of Mathematics in Africa South of the Sahara" [Manongod sa Uusipon kan Matematika sa Aprikang nasa Habagatan kan Sahara]. African Mathematical Union (in English). Retrieved Disyembre 5, 2020 – via State University of New York - Buffalo. Unknown parameter
|url-status=ignored (help); Check date values in:|access-date=(help) - ↑ Brooks, A.S.; Smith, C.C. (1987). "Ishango revisited: new age determinations and cultural interpretations" [Pagbisita utro sa [tulang nin] Ishango: bagong pagtataya sa gurang asin interpretasyon sa kultura]. The African Archaeological Review (in English). No. 5. pp. 65–78.
- ↑ Marshack, Alexander (1991). The Roots of Civilization [Ang Ugat ng Sibilisasyon] (in English). Colonial Hill, Mount Kisco, New York, Estados Unidos.
- ↑ Zaslavsky, Claudia (Enero 1992). "Women as the First Mathematicians" [Mga Babae bilang ang mga Unang Matematiko]. International Study Group on Ethnomathematics. Retrieved Disyembre 5, 2020. Unknown parameter
|url-status=ignored (help); Check date values in:|access-date=, |date=(help) - ↑ Robinson, Judy (1992). Not counting on Marshack: a reassessment of the work of Alexander Marshack on notation in the Upper Palaeolithic [Di umaasa kay Marshack: muling pagtingin sa gawa ni Alexander Marshack sa notasyon ng Mataas na Paleolitiko]. Journal of Mediterranean Studies. 2. pp. 1–16.
- ↑ "The Second Bone" [Ang Ikalawang Buto]. Royal Belgian Institute of Natural Sciences (in English). Archived from the original on Hunyo 23, 2016. Retrieved Disyembre 5, 2020. Unknown parameter
|url-status=ignored (help); Check date values in:|access-date=, |archive-date=(help)
